The concept of a ‘function’ – explained through a problem

Imagine a long distance runner who runs 10 miles in 50 minutes (averages 1 mile every 5 minutes).  Is it true that he has to have one stretch of 2 miles which is completed in EXACTLY 10 minutes?

Intuitively, there should be no reason that there needs to be a 2 mile stretch covered in 10 minutes.  After all, there are many ways to cover a 10 mile stretch in 50 minutes.

However, using our knowledge of functions (in particular, the mean value theorem), we will see that the above statement has to be true.

Solution Steps:

• We will define the TIME to cover a 2 mile stretch as a function – t(2).  The ‘t’ stands for time and t(2) means ‘time taken to run 2 miles’.  From this definition of a function, we see that :

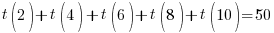
• Use the intermediate value theorem to prove that there must be one point (one two mile stretch) that is exactly 10.

Since the sum of the 5 values of our function is exactly 50, not all of them are greater than 10 (otherwise the sum would exceed 50) – and not all of them are less than 10  (otherwise the sum would be less than 50).

This means that there are (at least) two points (x and y) such that one is greater than 10 and one is less than 10. We can write this mathematically as:

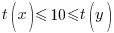
Using the mean value theorem, this means that there is a point (call it r ), that is between x and y such that:

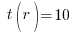
This shows that our distance runner will complete a (at least one) 2 mile stretch in exactly 10 minutes!  So – we solved a problem by defining a function for our problem domain. Once we had our function, we used a well known result for functions in general (the mean value theorem), to prove our problem statement.