Check out also – Problems In Advanced Math and Physics and Rare Finds in Special and General Relativity

Why are complex numbers so useful in the natural sciences?

Analyticity (harder to do without complex numbers)

Analytic functions can be expanded in Taylor series in their region of analyticity. Which means that, in that region, derivatives of all orders exist. This is important to physicists and applied mathematicians. With an expansion, one can find the co-efficients and arrive at a ‘number’ for the value of the function at a point (which, in the general case, is not always easy).

Now, prior to complex numbers, analyticity was difficult to establish. There was no consistent way except calculating all the order derivatives and seeing if they existed. With complex numbers, the magic is that if the FIRST order derivative of the complex function exists, then, the function is guaranteed to be analytic! So – all you do is – take your real function – write it’s complex equivalent – and check for the first derivative (which is essentially checking for two real derivatives via the Cauchy Riemann equations). If these two real derivatives exist – life is good – and you can safely expand the function around a point in the region of analyticity.

\frac {df}{dz}(z_0) = lim_{h->0} \frac{f(z_0 + h) - f(z)}{h}

Integration (also harder to do without complex numbers)

Certain integrals like \int_{-\infty}^{\infty} \frac{sin(x)}{x} are difficult to do in the real number system. In the complex world, thanks to contour integration, you can simply ‘extend’ the real function into complex space – and use the following useful theorems to calculate the integral.

  1. Closed Loop Theorem – \oint f(z) dz = 0
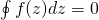
  2. Residue Theorem – \oint f(z) dz = 2\pi i \Sigma Residues

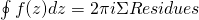
The connection with 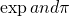\exp and \pi

This is probably the most magical thing about complex numbers. e^{i\pi} = -1 which is a specific case of Euler’s identity, e^{ix} = \cos(x) + i\sin(x) somehow connects two of the most important natural constants – e and \pi – with the simple introduction of an imaginary exponent.

This has far reaching consequences – and one can find infinite roots of unity using this identity. Infinite Roots! Of the innocent looking number 1 – which, as per REAL analysis, should have just one root – 1!

Summary

Next time someone asks you – What’s the big deal about complex numbers, throw this at them.  It has magically solved some of the toughest challenges facing physicists and applied mathematicians. It also magically connects completely unrelated natural constants.

Anuj holds professional certifications in Google Cloud, AWS as well as certifications in Docker and App Performance Tools such as New Relic. He specializes in Cloud Security, Data Encryption and Container Technologies.

Initial Consultation

Anuj Varma – who has written posts on Anuj Varma, Hands-On Technology Architect, Clean Air Activist.

 Twitter Linkedin