Open sets and limit points
- A set
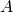 is open iff for every point
is open iff for every point 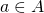 , there exists a
, there exists a 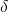 such that the neighborhood
such that the neighborhood 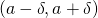 surrounding
surrounding  is completely contained within (is a subset of)
is completely contained within (is a subset of) 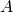 .
. - A point
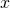 is a limit point of a set
is a limit point of a set 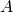 iff given any
iff given any  , all neighborhoods
, all neighborhoods 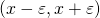 intersect the set
intersect the set 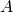 in some point other than
in some point other than 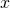 . Note that
. Note that 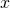 need not be a point in
need not be a point in 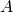 .
.
Let ![]() be a point in
be a point in ![]() . Since
. Since ![]() is open, there is a number
is open, there is a number ![]() such that
such that ![]() .
.
We now show ![]() is a limit point of
is a limit point of ![]() . To that end, let
. To that end, let ![]() be given. We may assume, without loss of generality, that
be given. We may assume, without loss of generality, that ![]() . Now,
. Now, ![]() , so
, so ![]() . Since
. Since ![]() intersects
intersects ![]() in a point other than
in a point other than ![]() , we conclude
, we conclude ![]() is a limit point.
is a limit point.
If ![]() , then
, then ![]() , so
, so ![]() . Openness already gives you an open
. Openness already gives you an open ![]() -interval around
-interval around ![]() , so you only need to worry about the case where
, so you only need to worry about the case where ![]() is smaller than that.
is smaller than that.
Leave a Reply